28 February 2011
23 February 2011
Perfect angular 'Surface' simulation - 12 XII
4*PI*R^2=S
4*PI*25=144
PIdx=1,44
dx=1,44/180=0,008 degree surface units(DSU)
DSU= see thickness of 'surface' per Degree in 3D Graphics !
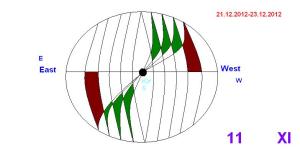
Nibiru is coming... get the Cross, get the third Point !
So, it's coming ! Coming soon, coming later - coming May !
We assume the Earth is not moving around its axis ! That's the cross...
I chase Nibiru. You see its first appearance at I, fires over russia and Australian disaster at II-III. You'll see Nibiru itself on the sky at point III with some strong winds for several days. You'll see it every day between points III-E !
What do we have here ?! - Getting the projection it's Othogonal. You now Orbit of a Planet - it's Elliptical. You see points of twisting on the picture. You need two or three Professional observations to take the exact Orbit of this Brown Dwarf Planet.
You know the vicinity of "a" and the Top of the Ellipse( point E ). This means you know the Exact Orbit of it ! No more Main Theories - just ONE ! The X center of the Elliptic Orbit is suggested a Black hole...
Finally, you see December 2012. The telescopes are already there on the South pole, owned by the space Agencies, waiting for it. It will get back through Z axis UP after this date, I still don't know the back Orbit on my Pictures.
Point E is kind of a third Lagrangian point !
Nibiru is 5 times bigger than the Moon !
As you see the angularity lines, they are rotated. If assumed these are forces, nothing that disaster alike will happen :) . This, on other side doesn't allow us to say it's third "static" Lagrangian point.
It is coming !!!
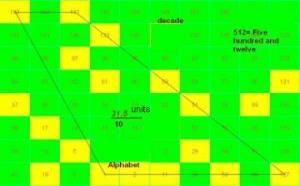
The Eleven (11 or XI ) digit
11=1+2+3+5
1 as Smallest part
2 as Direction
3 as Constructive part Digits!
5 as Wave
7 as the Circle
10 as Twisting ( Theory of Relativity ) + 1 Number!
1 as Smallest part
2 as Direction
3 as Constructive part Digits!
5 as Wave
7 as the Circle
10 as Twisting ( Theory of Relativity ) + 1 Number!
Fibonacci spiral - other point of view
Here is the original Fibonacci spiral:
Fibonacci spiral
My point of view:
As can be seen, points one and one determine the precise horizontal and one and two inclined straight lines tended to turn vertically. Thereafter, observations and logical reasoning are the other straight, "read" - "odd" elements in parallel determine the sequence-dependent horizontal and the other ("odd" - "read") will be approximations of parallelism of the first vertical (between the first two points) construction and always will slightly modify according to one another in order of increasing raw of Fibonacci!
Fibonacci spiral
My point of view:
As can be seen, points one and one determine the precise horizontal and one and two inclined straight lines tended to turn vertically. Thereafter, observations and logical reasoning are the other straight, "read" - "odd" elements in parallel determine the sequence-dependent horizontal and the other ("odd" - "read") will be approximations of parallelism of the first vertical (between the first two points) construction and always will slightly modify according to one another in order of increasing raw of Fibonacci!
Endless lattice of Einstein - 10
10 X
| | | | |
| | | | |
— — — — — — — —
| | | | |
— — — — — — — —
| | | | |
— — — — — — — —
| | | | |
— — — — — — — —
| | | | |
| | | | |
...continues from the first Posting !
Neper Epsilon vicinity to Integral
In three-dimensional convex polyhedron D, will have six two-dimensional view, and its surface will be characterized by a triple integral. Six views will be orthogonal projections, which may be given on the spiral Ulamov analogous to ABCD ...
Volume from the Age of Electronics until today !
The way one Microcontroller/Microprocessor works :
Example: 8052.com (classical site)
Sinusoid modeling of Volume:
Sinusoid modeling of Volume:
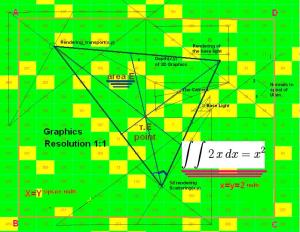
Lights and programming methods of 3d Graphics
1. Polynomials and polynomial equations
2. 3d computer graphics
3. Raster graphics
4. 3d rendering
RGB, CMYK
2. 3d computer graphics
3. Raster graphics
4. 3d rendering
RGB, CMYK
Special theory of Relativity on Ulam spiral
=> object on this scale (far from us), which glows with a light will stay in one place at the moment we see him!
=> object close to us will be seen three-dimensional (with directions)!
=> We can conditionally divide the light to "directional" and "distant" light
=> object close to us will be seen three-dimensional (with directions)!
=> We can conditionally divide the light to "directional" and "distant" light
Pi. Circles of space and space-time
1. For round fixtures Pi acquires a precise physical meaning
2. Pi is the final fraction in terms of perceived physical (mass-significant) matter:)
3. Fractional remainder of Pi goes to photons
4. Since C1 *, C2 *, C3 * are linear to spiral of prime numbers, it can be considered that the points of which they consist are ideal circles.They are still points.V Thus each circle with center of these points can be regarded as an ideal sphere. Finding such a circle in the sense of helix of prime numbers will lead to finding the exact final order of Pi in the physical sense:)
5. Physical meaning of the word - all tangible physical quantities that can be developed by triangles Lagrange
6. pi = (the circumference) / (diameter j)
7. pi ^ 2 = S / (4 * (r ^ 2))
8. => S area of the circle X is linearized in circumference X
9. r of this circle will be Distance
10. It is clear that will be mentioned for each r => face of this circle will be space
11. Length of a circle is area of the spiral of prime numbers. Face of the circle lies in the spiral space of prime numbers
12. This proves that if you can describe a circle around the speed-gravitational-BC-CD quadrangle, the intersection of the diagonals is indeed gravitationally breaking point
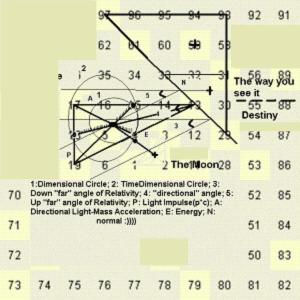
Circle of space
passes through points 4.15 and Summit 19-5
Circle of Time-space
passes through points 4,15 и 18

1. Center of the circle of space-time will be the center of the wrapping of the space-time
2. Pi is the final fraction in terms of perceived physical (mass-significant) matter:)
3. Fractional remainder of Pi goes to photons
4. Since C1 *, C2 *, C3 * are linear to spiral of prime numbers, it can be considered that the points of which they consist are ideal circles.They are still points.V Thus each circle with center of these points can be regarded as an ideal sphere. Finding such a circle in the sense of helix of prime numbers will lead to finding the exact final order of Pi in the physical sense:)
5. Physical meaning of the word - all tangible physical quantities that can be developed by triangles Lagrange
6. pi = (the circumference) / (diameter j)
7. pi ^ 2 = S / (4 * (r ^ 2))
8. => S area of the circle X is linearized in circumference X
9. r of this circle will be Distance
10. It is clear that will be mentioned for each r => face of this circle will be space
11. Length of a circle is area of the spiral of prime numbers. Face of the circle lies in the spiral space of prime numbers
12. This proves that if you can describe a circle around the speed-gravitational-BC-CD quadrangle, the intersection of the diagonals is indeed gravitationally breaking point
Circle of space
passes through points 4.15 and Summit 19-5

Circle of Time-space
passes through points 4,15 и 18

1. Center of the circle of space-time will be the center of the wrapping of the space-time
- 2. => Circumference of the space-time (O) / 2 times the radius of the circle of space-time (2R) = Pi perfectly just in the physical sense
3. O and 2R can be called ideal
4. That is, there will be two exact numbers that divide one another - they will have accurate figures and fractions will be able to take into account what is called in physics "negligible"
5. Here as a vital condition is what is the unit of cm for example, but ranging from C1 * and go through that Gravity should work in absolute terms!
6. If you enjoyed C1 * out that the physical meaning is not constant, there is dt
7. According to my theory Pi is constant,> these two triangles are interconnected as a system (eg, Earth-Moon) => they are expressed as a system (eg C1 *, C2 *, C3 * + c1 *, c2 *, c3 *), as in time => dt = 1 => PI = const in the physical sense
8. Proof is that the force of gravity F = M * g is always maintained in such a system
9. it can be expressed only through the mass of a body only through the mass of the other body, or a system as a whole both
- 2. => Circumference of the space-time (O) / 2 times the radius of the circle of space-time (2R) = Pi perfectly just in the physical sense
ABCD rectangle
Ulam spiral
Ulam spiral
From Wikipedia, the free encyclopedia
Jump to: navigation, search
The Ulam spiral, or prime spiral (in other languages also called the Ulam Cloth) is a simple method of visualizing the prime numbers that reveals the apparent tendency of certain quadratic polynomials to generate unusually large numbers of primes. It was discovered by the mathematician Stanislaw Ulam in 1963, while he was doodling during the presentation of a “long and very boring paper”[1] at a scientific meeting. Shortly afterwards, in an early application of computer graphics, Ulam with collaborators Myron Stein and Mark Wells used MANIAC II at Los Alamos Scientific Laboratory to produce pictures of the spiral for numbers up to 65,000.[2][1][3] In March of the following year, Martin Gardner wrote about the Ulam spiral in his Mathematical Games column;[1] the Ulam spiral featured on the front cover of the issue of Scientific American in which the column appeared.Ulam constructed the spiral by writing down a regular rectangular grid of numbers, starting with 1 at the center, and spiraling out:
He then circled all of the prime numbers and he got the following picture:
To his surprise, the circled numbers tended to line up along diagonal lines. The image below is a 200×200 Ulam spiral, where primes are black. Diagonal lines are clearly visible, confirming the pattern. Horizontal and vertical lines, while less prominent, are also evident.
All prime numbers, except for the number 2, are odd numbers. Since in the Ulam spiral adjacent diagonals are alternatively odd and even numbers, it is no surprise that all prime numbers lie in alternate diagonals of the Ulam spiral. What is startling is the tendency of prime numbers to lie on some diagonals more than others.
Tests so far confirm that there are diagonal lines even when many numbers are plotted. The pattern also seems to appear even if the number at the center is not 1 (and can, in fact, be much larger than 1). This implies that there are many integer constants b and c such that the function:
- f(n) = 4n2 + bn + c
Remarkably, in a passage from his 1956 novel The City and the Stars, author Arthur C. Clarke describes the prime spiral seven years before it was discovered by Ulam. Apparently, Clarke did not notice the pattern revealed by the Prime Spiral because he "never actually performed this thought experiment."[4]
According to Ed Pegg, Jr., the herpetologist Laurence M. Klauber proposed the use of a prime number spiral in finding prime-rich quadratic polynomials in 1932, more than thirty years prior to Ulam's discovery.[5]
Contents[hide] |
[edit] Hardy and Littlewood's Conjecture F
In their famous 1923 paper on the Goldbach Conjecture, Hardy and Littlewood stated a series of conjectures, one of which, if true, would explain some of the striking features of the Ulam spiral. This conjecture, which Hardy and Littlewood called “Conjecture F”, is a special case of the Bateman–Horn conjecture and asserts an asymptotic formula for the number of primes of the form ax2+bx+c. Rays emanating from the central region of the Ulam spiral making angles of 45° with the horizontal and vertical correspond to numbers of the form 4x2+bx+c with b even; horizontal and vertical rays correspond to numbers of the same form with b odd. Conjecture F provides a formula that can be used to estimate the density of primes along such rays. It implies that there will be considerable variability in the density along different rays. In particular, the density is highly sensitive to the discriminant of the polynomial, b2−16c.Conjecture F is concerned with polynomials of the form ax2+bx+c where a, b, and c are integers and a is positive. If the coefficients contain a common factor greater than 1 or if the discriminant Δ=b2−4ac is a perfect square, the polynomial factorizes and therefore produces composite numbers as x takes the values 0, 1, 2, ... (except possibly for one or two values of x where one of the factors equals 1). Moreover, if a+b and c are both even, the polynomial produces only even values, and is therefore composite except possibly for the value 2. Hardy and Littlewood assert that, apart from these situations, ax2+bx+c takes prime values infinitely often as x takes the values 0, 1, 2, ... This statement is a special case of an earlier conjecture of Bunyakovsky and remains open. Hardy and Littlewood further assert that, asymptotically, the number P(n) of primes of the form ax2+bx+c and less than n is given by
 is an odd prime not dividing a. The quantity ε is defined to be 1 if a+b is odd and 2 if a+b is even. The symbol
is an odd prime not dividing a. The quantity ε is defined to be 1 if a+b is odd and 2 if a+b is even. The symbol  is the Legendre symbol. A quadratic polynomial with A ≈ 11.3, currently the highest known value, has been discovered by Jacobson and Williams.[6][7]
is the Legendre symbol. A quadratic polynomial with A ≈ 11.3, currently the highest known value, has been discovered by Jacobson and Williams.[6][7][edit] Sacks spiral
Robert Sacks devised a variant of the Ulam spiral in 1994. In the Sacks spiral the non-negative integers are plotted on an Archimedean spiral rather than the square spiral used by Ulam, and are spaced so that one perfect square occurs in each full rotation. (In the Ulam spiral, two squares occur in each rotation.) Euler's prime-generating polynomial, x2−x+41, now appears as a single curve as x takes the values 0, 1, 2, ... This curve asymptotically approaches a horizontal line in the left half of the figure. (In the Ulam spiral, Euler's polynomial forms two diagonal lines, one in the top half of the figure, corresponding to even values of x in the sequence, the other in the bottom half of the figure corresponding to odd values of x in the sequence.)
Triangles of Lagrang:

Eight-bit processor based on prime numbers
Accumulator:
Х Х Х ХХХХX —> 1 2 3 - low bits
| | | | | | | |
1713117 5 3 2 1
Register R0:
Х Х Х Х Х Х Х Х
| 43 | 41 | 37 | 31 | 29 | 23 | 19 |
00000000 = 0 |
00000001 = 1 | “one“
00000010 = 2 | “two“
00000100 = 3 | “three“
00000110 = 4 | 3 two
00001000 = 5 | “four“
00001001 = 6 | 5 one
00010000 = 7 | “five“
00010001 = 8 | 7 one
00010010 = 9 | 7 two
00010100 = 10| 7 three
00100000 = 11| “six“
00100001 = 12| 11 one
01000000 = 13| “SEVEN“
01000001 = 14| 13 one
01000010 = 15| 13 two
01000100 = 16| 13 three
10000000 = 17| “EIGHT“
Every prime number, which is not low bit is able to be presented in more than one way.
It is always better to present one number with smaller bits.
Calculation rules
Sum:
Case А) ? no double bit:
01000100 = 16
+
00001001 = 6
=
01001101 = 22
Case B) ? the double bit is presented through lower bits:
01000100 = 16 = 13 three
+
00010100 = 10 = 7 three
=
01010100 =
+
00000100 = 00000011
=
01010111 = 26
01000000 = 13 = 13
+
01000001 = 14 = 13 one
=
01000001
+
01000000 = 00100010
=
01100011 = 27
01000001 = 14 = 13 one
+
01000010 = 15 = 13 two
=
01000011
+
01000000 = 00011000
=
00011011 = 29
We sum А and B, A>B
I. А+B=C+D , when C is a number including all significant bits no matter their repeating, and D consists only of double bits.
- D=E+F+… ; E, F ? numbers consisted only from one digit
Conclusion: Since the actual discharge means multiplication of the unit with a prime number, and because the numbers are hole, transformations II are actually bringing the numbers to end chain fractiones.
Substraction:
01000100 = 16 = 00100110 = 2+3+11
-
00001001 = 6 = 00000111 = 1 + 2 + 3
=
000010110 = 10
Substraction А from B, А>B
А and B are divided to significant bits with lower rates;
А-B = D-E ,E ?
The action is repeating until:
X=00000000 (0) или X=00000001 (1)
X=0 , the result is D
X=1, analogic -> try it yourself
Multiplication:
00001000 = 5 = 00000110 = 2+3
*
00001001 = 6 = 00000111 = 1 + 2 + 3
=
11000000 = 30 = 2*3*5 = 00000010
*
00000100
*
00001000
=
(2*3)*5
2*3
=
00000010
*
00000100
=
00000100
+
00000100
=
00000111=6
(2*3)*5
=
……….
Multiplication is alike sum !
…..
General conclusion: This kind of processor would be much faster and efficient.
Conclusion: One 9-bit processor should be much more precise at the point.
X Х Х Х ХХХХX —> 1 2 3
| | | | | | | | |
19171311 7 5 3 2 1
13 17 19 highest bits !
There is geometrical-physical matter !
1 is point, and 13+17+19=7*7 =circle*circle = Sphere
Labels:
8,
9,
bit,
circle,
digit,
math,
mathematics,
multiplication,
nature,
number,
prime,
processor,
sphere,
substraction,
sum
Theoretical 3-bit processor -> sum of prime numbers
Labels:
3,
bit,
calculate,
calculation,
digits,
efficiency,
interruption,
numbers,
prime,
processor,
theory,
three
Characteristic equations of the Chess game



The points-centres of the chess board must be projected on the pyramid...
Point 1: 5/6 from the foundation on the height of the pyramid
Point 2: 1/3 from the foundation on theheight of the pyramid
Explanation:
The inner squares of the board are situated on the upper wall of the half-cube, and the rest on the side walls. The down wall is without squares !
I1( Integral debute ) = А
I2 ( Integral mittelspiel ) = B – А
I3 ( Integral endspiel ) = C – B
А

B

C

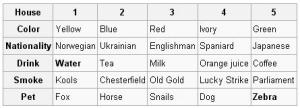
Einstein riddle
Now, who drinks water? Who owns the zebra? In the interest of clarity, it must be added that each of the five houses is painted a different color, and their inhabitants are of different national extractions, own different pets, drink different beverages and smoke different brands of American cigarets [sic]. One other thing: in statement 6, right means your right.– Life International, December 17, 1962
- There are five houses.
- The Englishman lives in the red house.
- The Spaniard owns the dog.
- Coffee is drunk in the green house.
- The Ukrainian drinks tea.
- The green house is immediately to the right of the ivory house.
- The Old Gold smoker owns snails.
- Kools are smoked in the yellow house.
- Milk is drunk in the middle house.
- The Norwegian lives in the first house.
- The man who smokes Chesterfields lives in the house next to the man with the fox.
- Kools are smoked in the house next to the house where the horse is kept. (should be "... a house ...", see Discussion section)
- The Lucky Strike smoker drinks orange juice.
- The Japanese smokes Parliaments.
- The Norwegian lives next to the blue house.
Solution
Subscribe to:
Posts (Atom)