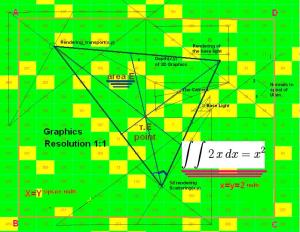
In three-dimensional convex polyhedron D, will have six two-dimensional view, and its surface will be characterized by a triple integral. Six views will be orthogonal projections, which may be given on the spiral Ulamov analogous to ABCD ...
Showing posts with label integral. Show all posts
Showing posts with label integral. Show all posts
23 February 2011
Neper Epsilon vicinity to Integral
In three-dimensional convex polyhedron D, will have six two-dimensional view, and its surface will be characterized by a triple integral. Six views will be orthogonal projections, which may be given on the spiral Ulamov analogous to ABCD ...
Characteristic equations of the Chess game



The points-centres of the chess board must be projected on the pyramid...
Point 1: 5/6 from the foundation on the height of the pyramid
Point 2: 1/3 from the foundation on theheight of the pyramid
Explanation:
The inner squares of the board are situated on the upper wall of the half-cube, and the rest on the side walls. The down wall is without squares !
I1( Integral debute ) = А
I2 ( Integral mittelspiel ) = B – А
I3 ( Integral endspiel ) = C – B
А

B

C

Subscribe to:
Comments (Atom)